Deep Learning MRI Image Restoration: Swin Transformer Architecture
Advanced image restoration framework for novel low-field MRI systems using Swin Transformers - Physics-based noise modeling, multi-slice processing, and joint denoising with 2× super-resolution
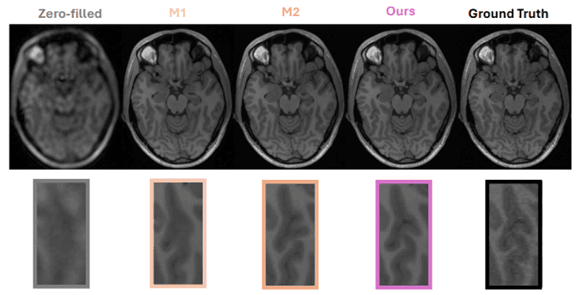
Abstract
This project implements a comprehensive deep learning framework for image restoration in Magnetic Resonance Imaging (MRI), specifically engineered for novel low-field MRI systems. The implementation leverages the Swin Transformer architecture (SwinIR) adapted for medical imaging applications, incorporating physics-based noise modeling, multi-slice temporal processing, and a composite loss function designed to preserve both structural fidelity and perceptual quality. The system addresses critical challenges in MRI reconstruction including noise amplification, spatial resolution enhancement, and magnetic field inhomogeneity artifacts.
Technical Context
Modern MRI systems face fundamental trade-offs between acquisition speed, signal-to-noise ratio (SNR), and spatial resolution. Novel low-field MRI architectures offer advantages in cost and accessibility but suffer from reduced SNR and increased susceptibility to field inhomogeneities. While traditional reconstruction methods rely on analytical approaches, deep learning-based methods can exploit rich statistical structures in MRI data for superior reconstruction quality.
This implementation presents a specialized adaptation of the Swin Transformer architecture for image restoration, incorporating domain-specific modifications for MRI data:
- Physics-based noise modeling from k-space measurements
- Multi-slice 3-channel processing for temporal coherence
- Composite loss functions balancing pixel-wise, perceptual, and frequency-domain fidelity
- Simultaneous denoising and 2× super-resolution in a unified framework
Network Architecture
Swin Transformer Foundation
The core architecture employs SwinIR, utilizing hierarchical Vision Transformers with shifted windows for efficient attention computation. The network comprises three primary components:
Shallow Feature Extraction
Input images are processed through a single 3×3 convolutional layer for low-level feature extraction:
where can be either single-channel (grayscale MRI slice) or 3-channel (three consecutive slices).
Deep Feature Extraction
The deep feature extraction module consists of multiple Residual Swin Transformer Blocks (RSTB). Each RSTB contains:
Window-based Self-Attention: Images are partitioned into non-overlapping 8×8 pixel windows. Multi-head self-attention is computed within each window:
where represents learnable relative position biases that encode spatial relationships.
Shifted Window Mechanism: Alternating blocks use shifted windows to enable cross-window connections, creating hierarchical representations that capture both local and global dependencies.
Feed-Forward Networks: Each attention block is followed by a two-layer MLP with GELU activation:
Residual Connections: Applied both within transformer blocks and across entire RSTBs via 3×3 convolutions for gradient flow and training stability.
The default configuration employs 6 RSTB layers, each containing 6 Swin Transformer blocks, with an embedding dimension of 180 and 6 attention heads per block.
Image Reconstruction Module
For simultaneous denoising and super-resolution, the reconstruction module employs nearest-neighbor interpolation followed by convolutional refinement:
This design reduces checkerboard artifacts compared to pixel-shuffle upsampling while maintaining computational efficiency.
Multi-Slice Temporal Processing
A key innovation for MRI data is 3-channel input processing representing consecutive slices:
- Channel 0: Previous slice (k-1)
- Channel 1: Current slice (k)
- Channel 2: Next slice (k+1)
This exploits strong anatomical correlation between adjacent MRI slices, enabling the network to leverage inter-slice consistency for improved reconstruction. During inference, only the middle channel (index 1) is extracted as the final output, while neighboring slices provide contextual information.
For edge cases (first and last slices), the current slice is replicated across all three channels.
Physics-Based Preprocessing Pipeline
MRI Noise Generation
A critical component is realistic MRI noise simulation. Unlike natural images where additive Gaussian noise suffices, MRI noise characteristics are fundamentally determined by k-space acquisition physics.
K-Space Noise Acquisition
Noise is directly measured from the MRI system by acquiring k-space data without RF excitation. This captures true noise distributions including:
- Thermal noise from receiver coils
- Electronic noise from amplifier chains
- Quantization noise from analog-to-digital conversion
Noise Volume Generation
For each training sample, a 3D noise volume is generated:
- Random sampling of noise lines from the measured k-space noise pool (without replacement)
- Reshaping into 3D k-space volume matching image dimensions
- Inverse Fourier transform to obtain image-space noise:
Field Inhomogeneity Warping
Low-field MRI systems are particularly susceptible to B₀ field inhomogeneities. The preprocessing pipeline simulates this through:
- Field Map Acquisition: Pre-measured B₀ field maps characterizing spatial variation in magnetic field strength
- Geometric Warping: The noise volume is resampled according to field maps using trilinear interpolation:
where is the field deviation, is the gyromagnetic ratio, and is the Jacobian determinant accounting for voxel compression/expansion.
- B₀ Bias Sampling: Random global field offset sampled from [0, 2] units to simulate inter-scan variability.
Spatial Resampling
The warped noise volume is resampled from acquisition resolution (1×1×1 mm³) to target resolution (1×1×3 mm³) using anti-aliased bilinear interpolation, with slices extracted to match training data geometry.
Image Transformations
Training images undergo several preprocessing steps:
-
Random Cropping: 240×240 pixel patches extracted during training for batch processing and data augmentation.
-
Histogram Matching: Each slice normalized to reference intensity range [0, 4.5]:
-
Morphological Masking: Inscribed square mask computed from noise support to focus reconstruction on anatomically relevant regions.
-
Degradation for Input: Source image downsampled by factor of 0.5 using bilinear interpolation to create low-resolution, noisy input.
-
SNR-Controlled Noise Addition: Noise scaled according to randomly sampled SNR ∈ [1.5, 2.5] during training (fixed at 2.0 for testing):
- Instance Normalization: Both source and target images normalized to zero mean and unit variance:
Composite Loss Function Design
The training objective employs a multi-component loss function balancing multiple image quality criteria:
Pixelwise Loss (L_pixel)
Charbonnier loss provides smooth gradients near zero while approximating L1:
where ensures differentiability. This enforces pixel-accurate reconstruction.
Weight: 2.0
Frequency Loss (L_freq)
To preserve k-space fidelity, frequency-domain loss is applied to both real and imaginary components of the 2D Fourier transform:
This is particularly important for MRI where k-space structure directly relates to acquisition physics.
Weight: 0.1
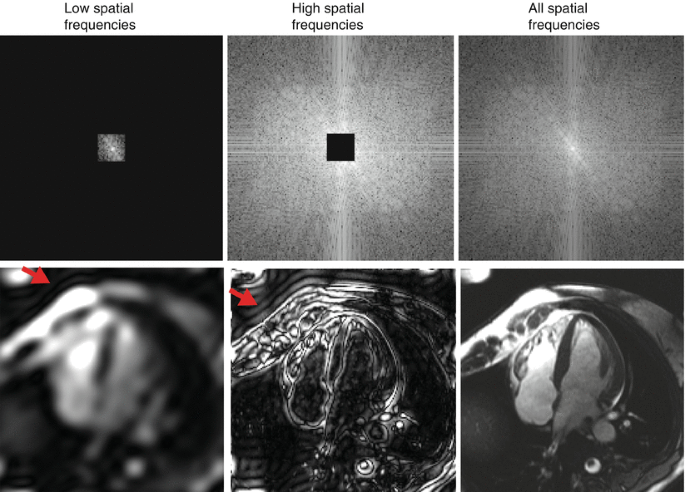
Frequency Domain Filtering in MRI. Top row: k-space data (Fourier domain) showing low frequencies (overall contrast and shape), high frequencies (edge details), and all frequencies (complete data). Bottom row: corresponding reconstructed MRI images demonstrating how low frequencies yield blurry images, high frequencies show edges, and all frequencies together create sharp, diagnostic-quality cardiac MRI scans. This illustrates the importance of the frequency-domain loss component in preserving k-space fidelity.
Perceptual Loss (L_percept)
Despite grayscale MRI images, perceptual loss using pre-trained VGG networks helps preserve anatomical textures:
where represents intermediate layer activations from VGG-16 (typically relu1_2, relu2_2, relu3_3).
Weight: 2.0
Gradient Loss (L_grad)
Spatial gradient preservation ensures edge sharpness and anatomical boundary definition:
Weight: 4.0
Total Loss
The final training objective:
Optional components (Edge Loss using Sobel operators, MS-SSIM) can be enabled via configuration for specific applications.
Inference Pipeline
Multi-Slice Assembly
During inference on 3D volumes:
-
Sequential Processing: For each slice k:
- Load slices k-1, k, k+1
- Apply histogram matching to [0, 4.5] range
- Stack into 3-channel input
- Normalize to zero mean, unit variance
-
Edge Handling:
- First slice (k=0): Use [k, k, k+1]
- Last slice (k=N-1): Use [k-1, k, k]
-
Batch Processing: Multiple slices processed in batches (default: 16) for computational efficiency.
Output Extraction
The network outputs a 3-channel reconstruction. Only the middle channel (index 1) is retained:
I_final = I_output[:, 1:2, :, :]
This channel corresponds to the reconstruction of the current slice, benefiting from contextual information from neighboring slices.
Super-Resolution
The output is automatically upsampled by 2× in both spatial dimensions through the network's reconstruction module, yielding images at double the input resolution.
Volume Export
Reconstructed slices are assembled into 3D volumes and exported as compressed NumPy arrays (.npz format) for further analysis or clinical review.
Training Infrastructure
The model is trained using modern deep learning infrastructure:
- Optimizer: AdamW with decoupled weight decay
- Batch Size: 16 slices per GPU
- Gradient Clipping: Maximum norm of 0.5 to prevent instability
- Learning Rate: Scheduled with warmup and cosine annealing
- Data Split: 70% training, 15% validation, 15% testing
- Framework: PyTorch Lightning for distributed training and automatic mixed precision
Training typically requires 100-200 epochs to converge, with early stopping based on validation PSNR.
Computational Architecture
The system leverages modern infrastructure:
- Hydra Configuration: Hierarchical configuration management for experiments
- PyTorch Lightning: Distributed training, automatic checkpointing, gradient accumulation
- Mixed Precision: FP16 training for memory efficiency and speed
- Gradient Checkpointing: Optional activation checkpointing for very deep models
Evaluation Metrics
The model is evaluated using a comprehensive suite of image quality metrics:
- PSNR (Peak Signal-to-Noise Ratio): Measures reconstruction accuracy
- SSIM (Structural Similarity Index): Assesses perceptual similarity
- MS-SSIM: Multi-scale structural similarity
- NRMSE (Normalized Root Mean Squared Error): Normalized pixel error
- VIF (Visual Information Fidelity): Information-theoretic quality metric
- LPIPS: Learned perceptual similarity using deep features
- DISTS: Deep image structure and texture similarity
Algorithmic Innovations
This framework introduces several key innovations tailored to MRI reconstruction:
Physics-Informed Noise Modeling
Unlike generic image denoising methods, the noise generation pipeline directly incorporates MRI acquisition physics:
- K-space noise statistics from actual hardware
- B₀ field inhomogeneity effects
- Geometric distortions from field gradients
This ensures the network learns to handle realistic degradations specific to the target MRI system.
Multi-Slice Coherence
The 3-channel architecture exploits anatomical continuity across slices, effectively implementing spatial-temporal regularization without explicit regularization terms. This is particularly valuable for MRI where slice thickness often exceeds in-plane resolution.
Hybrid Loss Function
The composite loss balances:
- Pixel accuracy (L_pixel, L_freq) for diagnostic fidelity
- Perceptual quality (L_percept) for visual assessment
- Edge preservation (L_grad) for anatomical boundary definition
This multi-objective optimization aligns better with clinical image quality requirements than any single metric.
Joint Denoising and Super-Resolution
By simultaneously addressing noise reduction and resolution enhancement, the network learns coupled priors that are more effective than sequential application of separate models.
Clinical Workflow Integration
Training Phase
- Acquire k-space noise measurements from target MRI system
- Measure B₀ field maps for the imaging protocol
- Generate synthetic noise library using field warping
- Train model on clinical MRI database (e.g., FastMRI knee dataset)
- Validate on held-out test set
Deployment Phase
- Export trained model to ONNX or TorchScript for production
- Integrate inference pipeline into MRI reconstruction software
- Process acquired images in real-time or batch mode
- Apply quality control checks using automated metrics
- Export reconstructed volumes in DICOM or research formats
Technical Limitations and Future Directions
Current Limitations
- Domain Specificity: Model is trained for specific anatomy (knee) and field strength; generalization requires additional training data
- Computational Cost: Inference requires GPU acceleration for real-time processing
- Grayscale Assumption: Perceptual loss using VGG requires channel replication; MRI-specific perceptual models could improve performance
Future Research Directions
- Uncertainty Quantification: Bayesian extensions or ensemble methods to provide confidence intervals on reconstructions
- k-Space Learning: Direct k-space processing rather than image-domain reconstruction
- Multi-Contrast Learning: Simultaneous processing of T1, T2, FLAIR sequences with cross-attention mechanisms
- Compressed Sensing Integration: Hybrid physics-based and learning-based reconstruction
- Real-Time Adaptation: Online learning to adapt to patient-specific motion or artifacts
Implementation Summary
This implementation presents a comprehensive deep learning framework for MRI image restoration specifically designed for novel low-field systems. By incorporating physics-based noise modeling, multi-slice temporal processing, and a carefully designed composite loss function, the approach addresses key challenges in MRI reconstruction including noise amplification, limited spatial resolution, and field inhomogeneity artifacts.
The Swin Transformer architecture provides an effective foundation for capturing both local and global image dependencies, while the custom preprocessing and training pipeline ensures the network learns realistic degradation patterns specific to the target MRI system. The modular design facilitates adaptation to different anatomies, field strengths, and clinical protocols.
As MRI technology continues to evolve toward more accessible, portable systems, deep learning-based reconstruction methods will play an increasingly important role in maintaining diagnostic image quality while reducing acquisition time and hardware complexity.
References
[1] Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L., & Timofte, R. (2021). SwinIR: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 1833-1844).
[2] Wang, S., Su, Z., Ying, L., Peng, X., Zhu, S., Liang, F., ... & Liang, D. (2016). Accelerating magnetic resonance imaging via deep learning. In 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI) (pp. 514-517). IEEE.
[3] Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., & Knoll, F. (2018). Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine, 79(6), 3055-3071.
[4] Johnson, J., Alahi, A., & Fei-Fei, L. (2016). Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision (pp. 694-711). Springer.
[5] Zhang, R., Isola, P., Efros, A. A., Shechtman, E., & Wang, O. (2018). The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 586-595).
[6] Ding, K., Ma, K., Wang, S., & Simoncelli, E. P. (2020). Image quality assessment: Unifying structure and texture similarity. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(5), 2567-2581.
[7] Zbontar, J., Knoll, F., Sriram, A., Murrell, T., Huang, Z., Muckley, M. J., ... & Lui, Y. W. (2018). fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839.