Uncovering Strong Lottery Tickets Using Continuously Relaxed Bernoulli Gates

Deep neural networks (DNNs) have achieved state-of-the-art performance across many domains, largely due to their over-parameterized nature. However, this comes at a cost—high memory usage, slow inference, and limited deployability on edge devices. In this work, we explore a new method to uncover Strong Lottery Tickets (SLTs) using a fully differentiable, training-free approach based on Continuously Relaxed Bernoulli Gates (CRBG).

---

Motivation

The Lottery Ticket Hypothesis (LTH) suggests that a small subnetwork within a large DNN, when trained in isolation, can match the performance of the original. A Strong Lottery Ticket (SLT) takes this further—achieving such performance without any weight updates.

Existing SLT methods like edge-popup require surrogate gradients or non-differentiable ranking, which limits scalability. Our method introduces a differentiable gating mechanism that learns sparse masks directly at initialization, keeping weights frozen.

---

Method Overview

The proposed method applies CRBGs to prune networks in both unstructured and structured fashions.

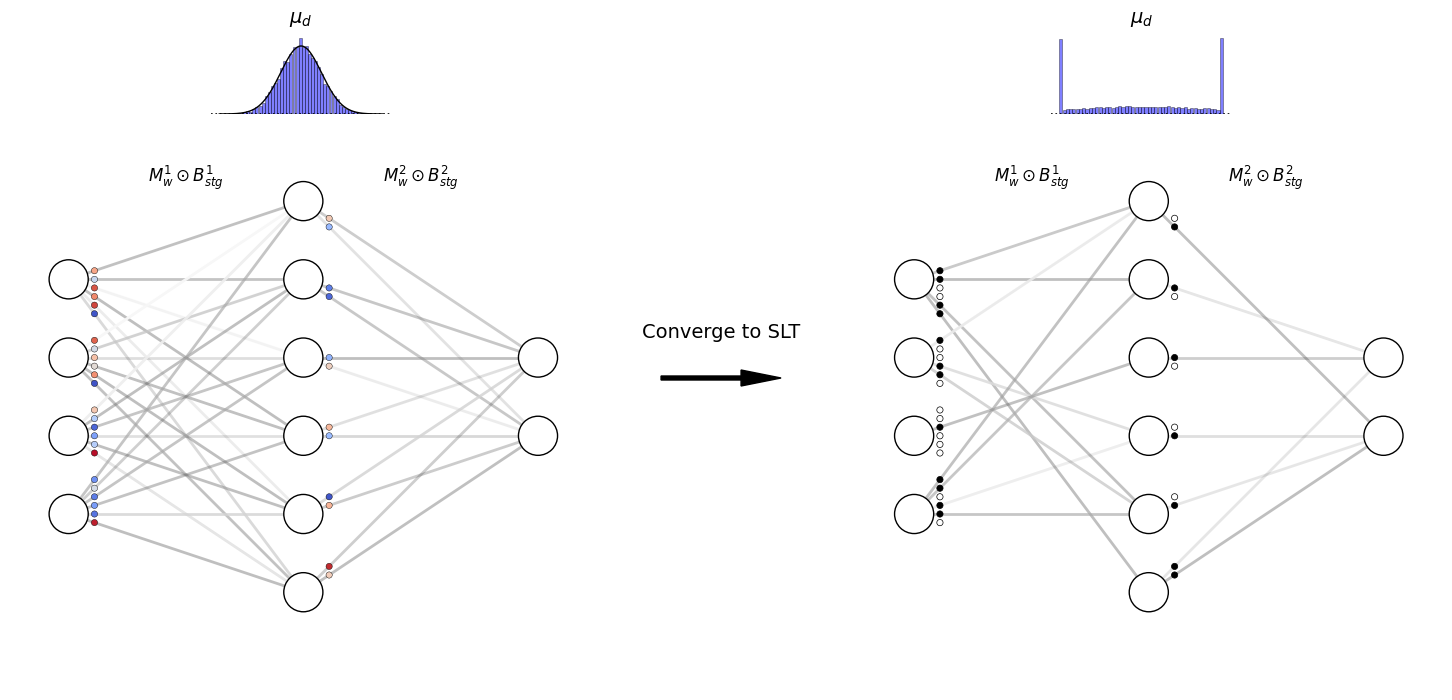Main architecture using Continuously Relaxed Bernoulli Gates

Unstructured Pruning

Each weight is gated using:

$$z_{ij}^l = \max(0, \min(1, \mu_{ij}^l + \epsilon_{ij}^l)), \quad \epsilon_{ij}^l \sim N(0, \sigma^2)$$

The output of layer $i$ becomes:

$$\widetilde{G}^{(i)}(x) = \sigma(B^{(i)} \odot W^{(i)} x)$$

where $B^{(i)}$ is the binary mask and $\odot$ denotes element-wise multiplication.

A sparsity-inducing regularization is applied:

$$R = \lambda \sum_{i,j,l} \Phi\left(\frac{\mu_{ij}^l}{\sigma}\right)$$

Structured Pruning

CRBGs are applied at the neuron level:

$$z_d^l = \max(0, \min(1, \mu_d^l + \epsilon_d^l))$$

Each layer output becomes:

$$h^{(i)} = g^{(i)} \odot \sigma(W^{(i)} h^{(i-1)})$$

The objective combines prediction loss and a sparsity penalty:

$$\min_{W^{(i)}, g^{(i)}} L(\{g^{(i)} \odot \sigma(W^{(i)} h^{(i-1)})\}) + \lambda \sum_{i=1}^{L} \|g^{(i)}\|_0$$

---

Initialization Strategy

We use a uniform distribution:

$$W \sim U[-\alpha, \alpha]$$

This avoids scaling heuristics like Xavier or Kaiming since weights remain fixed during the gating optimization.

---

Experiments

LeNet-300-100 on MNIST

• Achieved 88% test accuracy with 77% structured sparsity
• PreReLU used instead of ReLU to avoid unintentional sparsification
• Compared regularization strategies: induce-decision outperformed induce-sparse

CNNs on CIFAR-10

• ResNet-50: 83.1% accuracy, 91.5% weight sparsity
• Wide-ResNet50: 88% accuracy, 90.5% sparsity
• Observed higher sparsity in deeper layers, confirming redundancy in late-stage representations

Transformers

ViT-base

• 76% accuracy, 90% sparsity
• First strong lottery ticket discovered in vision transformers

Swin-T

• 80% accuracy, 50% sparsity

These results show our method scales to modern architectures and outperforms prior SLT discovery methods.

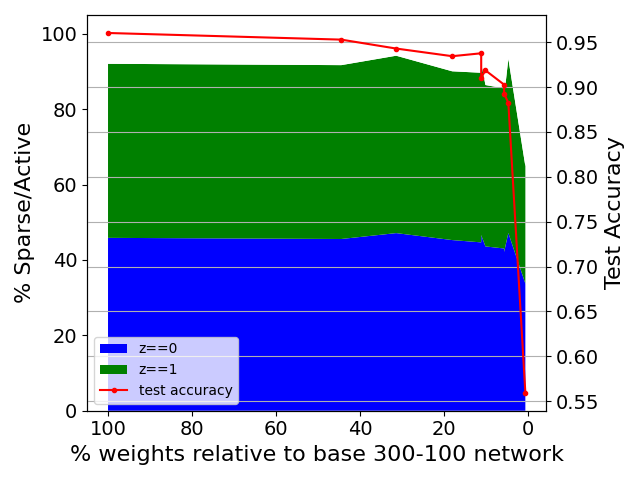Structured SLT discovery remains robust even as base network size shrinks

---

Comparison with State-of-the-Art

Method	Architecture	Accuracy	Sparsity	Trained Weights
Ours (CRBG)	LeNet-300-100	96%	45%	No
edge-popup (SLTH)	500-500-500-500	85%	50%	No
Sparse VD	512-114-72	98.2%	97.8%	Yes

---

Key Contributions

• Differentiable pruning using relaxed Bernoulli variables
• Supports both structured and unstructured sparsity
• Weight-free subnetwork discovery at initialization
• Applies to CNNs, FCNs, and Transformers
• Outperforms state-of-the-art in accuracy and sparsity trade-off

---

Future Work

Promising directions include:

• Adaptive regularization and variance learning
• Multi-level and hierarchical gating schemes
• Application to NLP, GNNs, and RNNs
• Theoretical analysis of convergence and expressivity
• Hardware-aware deployment for edge devices

---

Conclusion

This thesis proposes a scalable, training-free method to uncover Strong Lottery Tickets using Continuously Relaxed Bernoulli Gates. By enabling high sparsity and strong performance across diverse architectures, we take a step toward efficient, deployable, and interpretable deep learning.

The method demonstrates that sparse subnetworks exist at initialization and can be discovered through differentiable optimization, opening new possibilities for deploying neural networks on resource-constrained devices without sacrificing accuracy.

---

Full Thesis Document

---